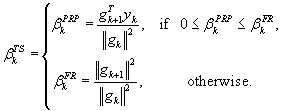A Hybrid Conjugate Gradient Algorithm for Unconstrained Optimization as a Convex Combination of Hestenes-Stiefel and Dai-Yuan
Neculai ANDREI
I C I Bucharest
(National Institute for R & D in Informatics)
Center for Advanced Modeling and Optimization
8-10 Averescu Blvd.
011455 Bucharest 1, Romania
nandrei@ici.ro
Abstract: In this paper we propose and analyze another hybrid conjugate gradient algorithm in which the parameter![]() is computed as a convex combination of
is computed as a convex combination of ![]() (Hestenes-Stiefel) and
(Hestenes-Stiefel) and ![]() (Dai-Yuan), i.e.
(Dai-Yuan), i.e. ![]() . The parameter
. The parameter ![]() in the convex combination is computed in such a way that the direction corresponding to the conjugate gradient algorithm is the Newton direction and the secant equation is satisfied. The algorithm uses the standard Wolfe line search conditions. Numerical comparisons with conjugate gradient algorithms using a set of 750 unconstrained optimization problems, some of them from the CUTE library, show that this hybrid computational scheme outperforms the Hestenes-Stiefel and the Dai-Yuan conjugate gradient algorithms as well as some other known hybrid conjugate gradient algorithms. Comparisons with CG_DESCENT by Hager and Zhang [17] and LBFGS by Liu and Nocedal [22] show that CG_DESCENT is more robust then our algorithm, and LBFGS is top performer among these algorithms.
in the convex combination is computed in such a way that the direction corresponding to the conjugate gradient algorithm is the Newton direction and the secant equation is satisfied. The algorithm uses the standard Wolfe line search conditions. Numerical comparisons with conjugate gradient algorithms using a set of 750 unconstrained optimization problems, some of them from the CUTE library, show that this hybrid computational scheme outperforms the Hestenes-Stiefel and the Dai-Yuan conjugate gradient algorithms as well as some other known hybrid conjugate gradient algorithms. Comparisons with CG_DESCENT by Hager and Zhang [17] and LBFGS by Liu and Nocedal [22] show that CG_DESCENT is more robust then our algorithm, and LBFGS is top performer among these algorithms.
Keywords: Unconstrained optimization, hybrid conjugate gradient method, Newton direction, numerical comparisons.
>>Full text
CITE THIS PAPER AS:
Neculai ANDREI, A Hybrid Conjugate Gradient Algorithm for Unconstrained Optimization as a Convex Combination of Hestenes-Stiefel and Dai-Yuan, Studies in Informatics and Control, ISSN 1220-1766, vol. 17 (1), pp. 55-70, 2008.
1. Introduction
In this paper let us consider the nonlinear unconstrained optimization problem
where ![]() is a continuously differentiable function, bounded from below. As we know, for solving this problem, starting from an initial guess
is a continuously differentiable function, bounded from below. As we know, for solving this problem, starting from an initial guess ![]() , a nonlinear conjugate gradient method, generates a sequence
, a nonlinear conjugate gradient method, generates a sequence ![]() as
as
where ![]() is obtained by line search, and the directions
is obtained by line search, and the directions ![]() are generated as
are generated as
In (3) ![]() is known as the conjugate gradient parameter,
is known as the conjugate gradient parameter, ![]() and
and ![]() . Consider
. Consider ![]() the Euclidean norm and define
the Euclidean norm and define ![]() . The line search in the conjugate gradient algorithms often is based on the standard Wolfe conditions:
. The line search in the conjugate gradient algorithms often is based on the standard Wolfe conditions:
where ![]() is a descent direction and
is a descent direction and ![]() Plenty of conjugate gradient methods are known, and an excellent survey of these methods, with a special attention on their global convergence, is given by Hager and Zhang [18]. Different conjugate gradient algorithms correspond to different choices for the scalar parameter
Plenty of conjugate gradient methods are known, and an excellent survey of these methods, with a special attention on their global convergence, is given by Hager and Zhang [18]. Different conjugate gradient algorithms correspond to different choices for the scalar parameter ![]() The methods of Fletcher and Reeves (FR) [15], of Dai and Yuan (DY) [11] and the Conjugate Descent (CD) proposed by Fletcher [14]:
The methods of Fletcher and Reeves (FR) [15], of Dai and Yuan (DY) [11] and the Conjugate Descent (CD) proposed by Fletcher [14]:
![]() ,
, ![]() ,
, ![]()
have strong convergence properties, but they may have modest practical performance due to jamming. On the other hand, the methods of Polak – Ribière [23] and Polyak (PRP) [24], of Hestenes and Stiefel (HS) [19] or of Liu and Storey (LS) [21]:
in general may not be convergent, but they often have better computational performances.
In this paper we focus on hybrid conjugate gradient methods. These methods are combinations of different conjugate gradient algorithms, mainly they being proposed to avoid the jamming phenomenon and to improve the performances of the above conjugate gradient algorithms. One of the first hybrid conjugate gradient algorithms has been introduced by Touati-Ahmed and Storey [27], where the parameter ![]() is computed as:
is computed as:
The PRP method has a built-in restart feature that directly addresses to jamming. Indeed, when the step ![]() is small, then the factor
is small, then the factor ![]() in the numerator of
in the numerator of ![]() tends to zero. Therefore,
tends to zero. Therefore, ![]() becomes small and the search direction
becomes small and the search direction ![]() is very close to the steepest descent direction
is very close to the steepest descent direction ![]() Hence, when the iterations jam, the method of Touati-Ahmed and Storey uses the PRP computational scheme.
Hence, when the iterations jam, the method of Touati-Ahmed and Storey uses the PRP computational scheme.
Another hybrid conjugate gradient method was given by Hu and Storey [20], where ![]() in (3) is:
in (3) is:
As above, when the method of Hu and Storey is jamming, then the PRP method is used instead.
The combination between LS and CD conjugate gradient methods leads to the following hybrid method:
The CD method of Fletcher [14] is very close to FR method. With an exact line search, CD method is identical to FR. Similarly, for an exact line search, LS method is also identical to PRP. Therefore, the hybrid LS-CD method with an exact line search has similar performances with the hybrid method of Hu and Storey.
Gilbert and Nocedal [16] suggested a combination between PRP and FR methods as:
Since ![]() is always nonnegative, it follows that
is always nonnegative, it follows that ![]() can be negative. The method of Gilbert and Nocedal has the same advantage of avoiding jamming.
can be negative. The method of Gilbert and Nocedal has the same advantage of avoiding jamming.
Using the standard Wolfe line search, the DY method always generates descent directions and if the gradient is Lipschitz continuously the method is global convergent. In an effort to improve their algorithm, Dai and Yuan [12] combined in a projective manner their algorithm with that of Hestenes and Stiefel, thus proposing the following two hybrid methods:
where ![]() . For the standard Wolfe conditions (4) and (5), under the Lipschitz continuity of the gradient, Dai and Yuan [12] established the global convergence of these hybrid computational schemes.
. For the standard Wolfe conditions (4) and (5), under the Lipschitz continuity of the gradient, Dai and Yuan [12] established the global convergence of these hybrid computational schemes.
In contrast to the hybrid methods ![]() and
and ![]() in this paper we propose another hybrid conjugate gradient where the parameter
in this paper we propose another hybrid conjugate gradient where the parameter ![]() is computed as a convex combination of
is computed as a convex combination of ![]() and
and ![]() . We selected these two methods to combine in a hybrid conjugate gradient algorithm because HS has good computational properties, on one side, and DY has strong convergence properties, on the other side. HS method automatically adjust
. We selected these two methods to combine in a hybrid conjugate gradient algorithm because HS has good computational properties, on one side, and DY has strong convergence properties, on the other side. HS method automatically adjust ![]() to avoid jamming, often this method performs better in practice than DY and we use this in order to have a good practical conjugate gradient algorithm. The structure of the paper is as follows. In section 2 we introduce our hybrid conjugate gradient algorithm and prove that it generates descent directions satisfying in some conditions the sufficient descent condition. Section 3 presents the algorithm and in section 4 we show its convergence analysis. In section 5 some numerical experiments and performance profiles of Dolan-Moré [13] corresponding to this new hybrid conjugate gradient algorithm versus some other conjugate gradient algorithms are presented. The performance profiles corresponding to a set of 750 unconstrained optimization problems in the CUTE test problem library [7], as well as some other unconstrained optimization problems presented in [1] show that this hybrid conjugate gradient algorithm outperforms the known hybrid conjugate gradient algorithms. However, the comparisons between our algorithm and CG_DESCENT by Hager and Zhang [17] show that CG_DESCENT is more robust. On the other hand, comparisons with LBFGS by Liu and Nocedal [22] show that limited memory LBFGS is top performer.
to avoid jamming, often this method performs better in practice than DY and we use this in order to have a good practical conjugate gradient algorithm. The structure of the paper is as follows. In section 2 we introduce our hybrid conjugate gradient algorithm and prove that it generates descent directions satisfying in some conditions the sufficient descent condition. Section 3 presents the algorithm and in section 4 we show its convergence analysis. In section 5 some numerical experiments and performance profiles of Dolan-Moré [13] corresponding to this new hybrid conjugate gradient algorithm versus some other conjugate gradient algorithms are presented. The performance profiles corresponding to a set of 750 unconstrained optimization problems in the CUTE test problem library [7], as well as some other unconstrained optimization problems presented in [1] show that this hybrid conjugate gradient algorithm outperforms the known hybrid conjugate gradient algorithms. However, the comparisons between our algorithm and CG_DESCENT by Hager and Zhang [17] show that CG_DESCENT is more robust. On the other hand, comparisons with LBFGS by Liu and Nocedal [22] show that limited memory LBFGS is top performer.
REFERENCES
- ANDREI, N., Test Functions for Unconstrained Optimization, http://www.ici.ro/ camo/neculai/HYBRID/evalfg.for
- ANDREI, N., Scaled Conjugate Gradient Algorithms for Unconstrained Optimization, Computational Optimization and Applications, 38 (2007), pp. 401-416.
- ANDREI, N., Scaled Memoryless BFGS Preconditioned Conjugate Gradient Algorithm for Unconstrained Optimization, Optimization Methods and Software, 22 (2007), pp. 561-571.
- ANDREI, N., A Scaled BFGS Preconditioned Conjugate Gradient Algorithm for Unconstrained Optimization, Applied Mathematics Letters, 20 (2007), pp. 645-650.
- ANDREI, N., Numerical Comparison of Conjugate Gradient Algorithms for Unconstrained Optimization, Studies in Informatics and Control, 16 (2007), pp. 333-352.
- BIRGIN, E., and J.M. MARTÍNEZ, A Spectral Conjugate Gradient Method for Unconstrained Optimization, Applied Math. and Optimization, 43, 2001, pp. 117-128.
- BONGARTZ, I., A.R. CONN, N.I.M. GOULD and P.L. TOINT, CUTE: Constrained and Unconstrained Testing Environments, ACM Trans. Math. Software, 21, 1995, pp. 123-160.
- DAI, Y.H., New Properties of a Nonlinear Conjugate Gradient Method, Numer. Math., 89 (2001), pp.83-98.
- DAI, Y.H., and L.Z. LIAO, New Conjugacy Conditions and Related Nonlinear Conjugate Gradient Methods, Appl. Math. Optim., 43 (2001), pp. 87-101.
- DAI, Y.H., HAN J.Y., LIU G.H., SUN D.F., YIN .X. and YUAN Y., Convergence Properties of Nonlinear Conjugate Gradient Methods, SIAM Jurnal on Optimization 10 (1999), pp. 348-358.
- DAI, Y.H., and Y. YUAN, A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property, SIAM J. Optim., 10 (1999), pp. 177-182.
- DAI, Y.H., and Y. YUAN, An Efficient Hybrid Conjugate Gradient Method for Unconstrained Optimization, Ann. Oper. Res., 103 (2001), pp. 33-47.
- DOLAN, E.D., and J.J. MORÉ, Benchmarking Optimization Software with Performance Profiles, Math. Programming, 91 (2002), pp. 201-213.
- FLETCHER, R., Practical Methods of Optimization, vol. 1: Unconstrained Optimization, John Wiley & Sons, New York, 1987.
- FLETCHER, R., and C. REEVES, Function Minimization by Conjugate Gradients, Comput. J., 7 (1964), pp.149-154.
- GILBERT, J.C., and J. NOCEDAL, Global Convergence Properties of Conjugate Gradient Methods for Optimization, SIAM J. Optim., 2 (1992), pp. 21-42.
- HAGER, W.W., and H. ZHANG, A New Conjugate Gradient Method with Guaranteed Descent and An Efficient Line Search, SIAM Journal on Optimization, 16 (2005), pp. 170-192.
- HAGER, W.W., and H. ZHANG, A Survey of Nonlinear Conjugate Gradient Methods, Pacific journal of Optimization, 2 (2006), pp.35-58.
- HESTENES, M.R., and E.L. STIEFEL, Methods of Conjugate Gradients for Solving Linear Systems, J. Research Nat. Bur. Standards, 49 (1952), pp.409-436.
- HU, Y.F., and C. STOREY, Global Convergence Result for Conjugate Gradient Methods, J. Optim. Theory Appl., 71 (1991), pp.399-405.
- LIU, Y., and C. STOREY, Efficient Generalized Conjugate Gradient Algorithms, Part 1: Theory, JOTA, 69 (1991), pp.129-137.
- LIU, D.C., J. NOCEDAL, On the Limited Memory BFGS Method for Large Scale Optimization, Mathematical Programming, Vol. 45 (1989), pp.503-528.
- POLAK, E. and G. RIBIERE, Note sur la convergence de directions conjuguée, Rev. Francaise Informat Recherche Operationelle, 3e Année 16 (1969), pp. 35-43.
- POLYAK, B.T., The Conjugate Gradient Method in Extreme Problems, USSR Comp. Math. Math. Phys., 9 (1969), pp. 94-112.
- POWELL, M.J.D., Nonconvex Minimization Calculations and the Conjugate Gradient Method, in Numerical Analysis (Dundee, 1983), Lecture Notes in Mathematics, Vol. 1066, Springer-Verlag, Berlin, 1984, pp. 122-141.
- SHANNO, D.F., and K.H. PHUA, Algorithm 500, Minimization of Unconstrained Multivariate Functions, ACM Trans. on Math. Soft., 2, 1976, pp. 87-94.
- TOUATI-AHMED, D., and C. STOREY, Efficient Hybrid Conjugate Gradient Techniques, J. Optim. Theory Appl., 64 (1990), pp. 379-397.
- ZHANG, J.Z., N.Y. DENG and L.H. CHEN, New Quasi-Newton Equation and Related Methods for Unconstrained Optimization, J. Optim. Theory Appl., 102 (1999), pp. 147-167.
- YABE, H., and M. TAKANO, Global Convergence Properties of Nonlinear Conjugate Gradient Methods with Modified Secant Condition, Computational Optimization and Applications, 28 (2004), pp. 203-225.
 Studies in Informatics and Control – ICI Bucharest
Studies in Informatics and Control – ICI Bucharest