Sparse Matrix Techniques in Scientific Computing
Aurelian NICOLA, Constantin POPA
Ovidius University
Blvd. Mamaia 124, 900527 Constanta, Romania
{anicola, cpopa}@univ-ovidius.ro
Abstract: Although the most important and relevant part of the scientific activity of Dr. Neculai Andrei is related to the design of efficient algorithms and software products for optimization problems, his first book, written in 1983 was devoted to sparse matrices and some of their applications in scientific computing. This is why we decided to present in our contribution some developments that we made in this direction, in the context of Matlab software, and 25 years after Neculai Andrei’s book. The paper presents the design and efficient implementation of some sparse matrix codes for numerical solution of a 2D convection-diffusion-reaction problem, by a preconditioned CG algorithm.
Keywords: Sparse matrices, scientific computing, convection-diffusion-reaction problems, multigrid algorithms, preconditioned CG algorithm.
Aurelian Nicola was born on August 17, 1973 in Constanta, Romania. He graduated from University of Constanta – Faculty of Mathematics and Computer Science in 1996 and obtained his PhD in 2005. Since 2006 he has held a lecturer position in Applied Mathematics at Ovidius University of Constanta, Romania – Faculty of Mathematics and Computer Science. His current research interests are: preconditioning techniques for finite element and finite differences discretizations of boundary value problems and iterative methods for solving sparse linear systems. He published 1 book, 1 paper in ISI quoted journal and more than 6 papers in other refereed journals or international conferences proceedings.
Constantin Popa was born on October 10, 1956 in Bucharest, Romania. He graduated the Faculty of Mathematics from University of Bucharest in 1981 and obtained his PhD in 1995. Since 2000 he has been a full professor in Applied Mathematics at the Faculty of Mathematics and Computer Science from Ovidius University of Constanta, Romania, where he is also heading the Department on Computer Science and Numerical Methods. His current research interests are: algebraic reconstruction techniques in Computerized Tomography, preconditioning techniques for finite element and finite differences discretizations of boundary value problems, iterative methods for least-squares formulations of linear systems of equalities and inequalities (projection algorithms), inverse problems – regularization techniques and methods for approximating the minimal norm solution of first kind integral equations. He published 4 books, 25 papers in ISI quoted journals and more than 40 papers in other refereed journals or international conferences proceedings. Some of his results have been cited in more than 25 papers.
>>Full text
CITE THIS PAPER AS:
Aurelian NICOLA, Constantin POPA, Sparse Matrix Techniques in Scientific Computing, Studies in Informatics and Control, ISSN 1220-1766, vol. 18 (1), pp. 33-38, 2009.
1. Introduction
We shall consider in this paper the (stationary) 2D convection-diffusion-reaction problem
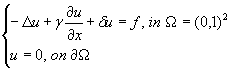 , (1)
, (1)
where ![]() and
and ![]() are such that a unique solution exists. For
are such that a unique solution exists. For ![]() a fixed integer, we discretized the domain
a fixed integer, we discretized the domain ![]() ,
,

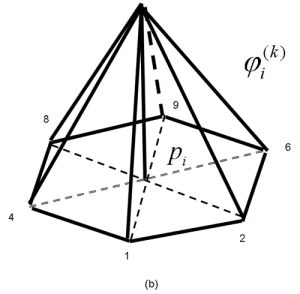 Figure1. Domain discretization.
Figure1. Domain discretization.
with ![]() uniformly distributed grid points and
uniformly distributed grid points and ![]() the mesh size of the discretization (see Figure 1(a) for k=2). We discretized the problem (1) by the Finite Element Method, using standard piecewise linear functions
the mesh size of the discretization (see Figure 1(a) for k=2). We discretized the problem (1) by the Finite Element Method, using standard piecewise linear functions ![]() as in Figure 1 (b) (see also for details [5, 6]). The
as in Figure 1 (b) (see also for details [5, 6]). The ![]() associated linear system
associated linear system
is nonsymmetric, positive definite, big (because the approximation error is of order ![]() , which means that we need an enough big value of
, which means that we need an enough big value of ![]() – and thus of
– and thus of ![]() , for an enough good approximation) and sparse (because of the special discretization of the problem domain in Figure 1(a) the matrix
, for an enough good approximation) and sparse (because of the special discretization of the problem domain in Figure 1(a) the matrix ![]() has at most 7 nonzero entries on each row). From these view points, direct methods are not recommended for solving (2). And, unfortunately, the “ill-conditioning” of the system matrix
has at most 7 nonzero entries on each row). From these view points, direct methods are not recommended for solving (2). And, unfortunately, the “ill-conditioning” of the system matrix ![]() produces a (very) slow convergence for classical iterative solvers (as e.g. CG; see for details [2, 3, 4]). One way to overcome this difficulty is to consider preconditioning techniques for (2). Such a method will be described in the next section of the paper.
produces a (very) slow convergence for classical iterative solvers (as e.g. CG; see for details [2, 3, 4]). One way to overcome this difficulty is to consider preconditioning techniques for (2). Such a method will be described in the next section of the paper.
REFERENCES
- Andrei, N., C. Rasturnoiu, Sparse matrices and applications (in romanian), Editura Tehnica, Bucuresti, 1983.
- Bjorck, A., Numerical Methods for Least Squares Problems, SIAM Philadelphia, 1996.
- Briggs, L. W. et al., A Multigrid Tutorial, SIAM Philadelphia, 1987.
- Griebel, M., Multilevel algorithms considered as iterative methods on semidefinite Systems, SIAM J. Sci. Comput., 15(3) (1994), pp. 547-565.
- Hackbusch, W., Elliptic Differential Equations. Theory and Numerical Treatment, Springer-Verlag, Berlin, 1987.
- Marchouk, G., V. Agochkov, Introduction aux Methodes des Elements Finis, Editions MIR, Moscou, 1985.
- Oden, J. T., J.N. Reddy, An Introduction to the Mathematical Theory of Finite Elements, John Wiley and Sons, Inc., 1976.
- Nicola, A., C. Popa, Preconditioning by an extended matrix technique for convection-diffusion-reaction equations, to appear in Rev. Roum. d’Analyse Numer. et Theorie d’Approx.
 Studies in Informatics and Control – ICI Bucharest
Studies in Informatics and Control – ICI Bucharest