Solving a Distribution Network Design Problem by
Combining Ant Colony Systems and
Lagrangian Relaxation
Carolina LAGOS1,*, Fernando PAREDES2, Stefanie NIKLANDER3,4, Enrique CABRERA5
1 Pontificia Universidad Católica de Valparaíso, Chile
carolina.lagos.c@mail.pucv.cl
2 Universidad Diego Portales, Escuela de Ingeniería Industrial, Chile
fernando.paredes@udp.cl
3 Universidad Autónoma de Chile, Chile
4 Universidad Científica del Sur, Peru
sniklander@gmail.com
5 Universidad de Valparaíso, CIMFAV, Chile
enrique.cabrera@uv.cl
Abstract: Distribution network design (DND) attempts to integrate tactical issues such as inventory policies and/or vehicle routing decisions with strategic ones such as the problem of locating facilities and allocate customers to such facilities. When inventory policy decision making is considered the problem is also known as inventory location modelling (ILM) problem. During the last two decades, mathematical programming as well as (meta-)heuristic approaches have been considered to address different DND problem. In this article we consider a hybrid algorithm of Lagrangian Relaxation and artificial ants to solve an ILM problem previously proposed in the literature. We use ACS to allocate customers to a subset of warehouses that is previously generated by the Lagrangian relaxation. Results show that the hybrid approach is quite competitive, obtaining near-optimal solutions within an acceptable time.
Keywords:Distribution Network Design, Matheuristics, Ant Colony Optimization, Lagrangian Relaxation.
>>Full text<<
CITE THIS PAPER AS:
Carolina LAGOS*, Fernando PAREDES, Stefanie NIKLANDER, Enrique CABRERA, Solving a Distribution Network Design Problem by Combining Ant Colony Systems and Lagrangian Relaxatio, Studies in Informatics and Control, ISSN 1220-1766, vol. 24 (3), pp. 251-260, 2015. https://doi.org/10.24846/v24i3y201502
- Introduction
The location-allocation problem is an important problem in logistics. The main goal is to find the best possible combination of facility locations (among a set of possible locations) to serve a set of customers, which must be allocated so that their demand may be fully satisfied by the installed facilities. This problem is, clearly, at strategic level as once the decision on what locations should be installed is made, it is very difficult to reverse such a decision because of the time and cost that such changes would imply. These class of problems have been widely studied in the literature ([1, 3, 8, 9, 10, 14, 34), and a variety of techniques have been proposed so far to solve it (for a comprehensive survey please see [21]).
During the last two decades, several authors have pointed out the importance of including tactical aspects such as inventory and transportation decisions within the same model that is used to solve the strategic problems [24, 30, 31, 32, 15, 35, 36, 39]. This is because sequential approaches, i.e. those that solve sequentially the strategic, tactical and operational problems, have been proved to lead to sub-optimal solutions, as the quality of the solution at each level will always depends on the quality of the solutions obtained in previous levels.
When inventory policies are included within the location-allocation model, the resulting model is known as Inventory Location Model (ILM). Several ILM have been proposed in the literature, being the main difference between them the inventory policy that is considered (see Section 2 for a short survey on ILM). In this article, we have considered the ILM proposed by [32].
In their article, authors propose a cross-level model that incorporates a continuous review inventory policy. In their proposed model storage space at each facility is limited and a capacity constraint over the distribution vehicles is applied. These conditions make the problem more realistic as they model common situations in logistics. It also makes this problem harder to solve though. The resulting model is nonlinear and includes both integer and continuous decision variables.
The model considers inventory control as well as facility location decision making. Two capacity constraints are considered: a limit over the size of the lot for the incoming orders to each facility and; a stochastic bound to the inventory capacity. In their article, authors solution approach consists of a Lagrangian relaxation and the well-known sub-gradient method, combined with a simple 2k-opt heuristic. Miranda et. al. [32] highlights the fact that reducing capacity of inventory does not necessarily means that the number of facilities to be installed must increase. In fact, order size reduction leads to an optimal customer allocation, reducing total system cost.
The mathematical model presented in [32] we consider in this study is as follows. Let W be the set of possible warehouse locations and i∈W be the i -th available warehouse in W . Let C be the set of customers to be allocated to selected warehouses i∈W+⊂W . As we mentioned before, a (Qi,RPi) inventory policy is considered. When the inventory level falls below RPi level in warehouse i , Qi items are ordered. LTi time units after the order Qi is triggered the items are received.
This is known as lead time. A probability of 1−α is considered to ensure a level of service for the system. This means that, with probability of (1−α), units below RPi are enough to satisfy customers demand during the lead time. Stock-out is produced otherwise. This leads to the following constraint:
![]()
where stochastic demand during lead time at warehouse i is denoted by (SD(LTi)) . Miranda et. al. [32] assumes a normally distributed demand which allows them to determine
![]()
Z1−α corresponds to standard normal distribution, Di and Vi are the total demand and the total variance at warehouse i , respectively. Let HCi be the holding cost and OCi be the order cost associated to warehouse i . Thus the inventory cost is
![]()
Fi denotes the fixed cost of opening warehouse i while RCij and TCij are the transportation unit cost and the fixed transportation cost between warehouse i and customer j , respectively. Thus, the goal is to minimise the total system cost that can be expressed as follows
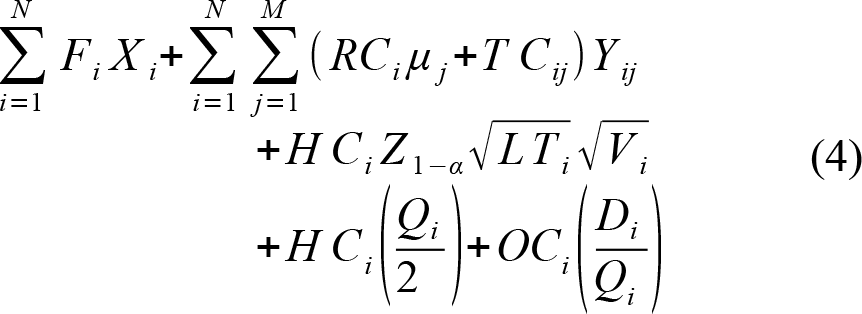
where µf is the customer j mean demand, N and M are the number of available warehouses and the number of customers, respectively. Miranda et. al. [32] proposes two constraints associated to order quantity Qi . The first one states the Qi must be less or equal that an arbitrary value Qub . The second one fixes the maximum inventory level for each warehouse as follows
![]()
which can be restated as
![]()
Additional constraints are:
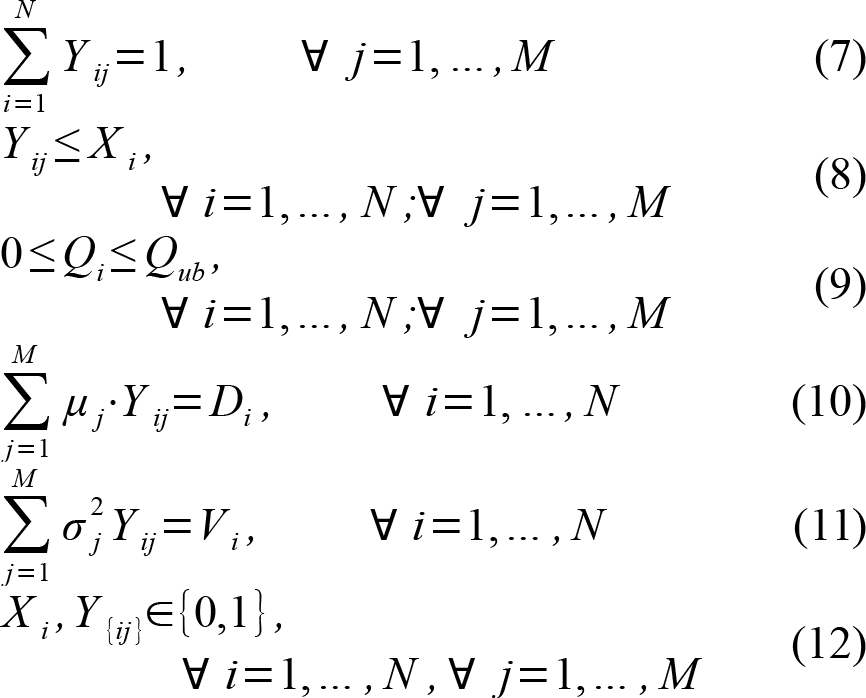
Equation (7) states that demand of customer i is fully satisfied by the system. Equation (8) ensures that customers are allocated only to installed warehouses. Equation (9) provides a valid range for Qi. Equations (10) and (11) set the total demand Di and total variance Vi for warehouse i based on the allocation variable Yij.
Finally Equation (12) states that decision variables X and Y are binary variables, which make this problem much harder to solve.
REFERENCES
- AL-SULTAN, K. S. M. A. AL-FAWZAN, A Tabu Search Approach to the Uncapacitated Facility Location Problem. Ann of Op. Res. vol. 86, 1999, pp. 91-103.
- ARMENTANO, V. A., A. L. SHIGUEMOTO, L. A. LOKKETANGEN, Tabu Search with Path Relinking for an Integrated Production-Distribution Problem. Comp. Op. Res., vol. 38(8), 2011, pp. 1199-1209.
- AROSTEGUI, M. A., S. N. KADIPASAOGLU, B. M. KHUMAWALA, An Empirical Comparison of Tabu Search, Simulated Annealing, and Genetic Algorithms for Facilities Location Problems. Intl. J. Prod. Ec., vol. 103(2), 2006, pp. 742-754.
- ASKIN, R. G., I. BAFFO, M. XIA, Multicommodity Warehouse Location and Distribution Planning with Inventory Consideration. Intl. J. Prod. Res., vol. 52(7), 2014, pp. 1897-1910.
- BADRI, H., M. BASHIRI, T. H. HEJAZI, Integrated Strategic and Tactical Planning in a Supply Chain Network Design with a Heuristic Solution Method. Comp. & Op. Res., vol. 40(4), 2013, pp. 1143-1154.
- BARAHONA, F., F. A. CHUDAK, Nearoptimal Solutions to Large-scale Facility Location Problems. Discrete Optimization, vol. 2(1), 2005, pp. 35-50.
- BARD, J. F., N. NANANUKUL, A Branch-and-Price Algorithm for an Integrated Production and Inventory Routing Problem. Comp. & Op. Res., vol. 37(12), 2010, pp. 2202-2217.
- BEASLEY, J. E., A Note on Solving Large p-Median Problems. E. J. of Op. Res., vol. 21, 1985, pp. 270-273.
- BEASLEY, J. E., An Algorithm for Solving Large Capacitated Warehouse Location Problems. E. J. Op. Res., vol. 33, 1988, pp. 314-325.
- BEASLEY, J. E., Lagrangean Heuristics for Location Problems. E. J. Op. Res., vol. 65, 1993, pp. 383-399.
- BERMAN, O., D. KRASS, M. M. TAJBAKHSH, A Coordinated Location Inventory Model. E. J. Op. Res., vol. 217(3), 2012, pp. 500-508.
- BRADLEY, J. R., B. C. ARNTZEN, The Simultaneous Planning of Production, Capacity, and Inventory in Seasonal Demand Environments. Operations Research, vol. 47(6), 1999, pp. 795-806.
- BULLNHEIMER, B., R. F. HARTL, C. STRAUSS, An Improved Ant System Algorithm for the Vehicle Routing Problem. Annals of Operations Research, vol. 89(0), 1999, pp. 319-328.
- CABRERA, G. G., E. CABRERA, R. SOTO, J. M. RUBIO, B. CRAWFORD, F. PAREDES, A Hybrid Approach using an Artificial Bee Algorithm with Mixed Integer Programming Applied to a Large-scale Capacitated Facility Location Problem. Mathematical Problems in Engineering, vol. 2012, 14 pages, Article ID 954249.
- CABRERA, G. G., E. CABRERA, R. SOTO, J. M. RUBIO, B. CRAWFORD, F. PAREDES, Solving a Novel Inventory Location Model with Stochastic Constraints and Inventory Control Policy. Mathematical Problems in Engineering, vol. 2013, 12 pages, 2013. Article ID 670528.
- DASKIN, M. S., Network and Discrete Location: Models, Algorithms, and Applications. Wiley-Interscience, 1st edition, 1995.
- DASKIN, M. S., C. R. COULLARD, Z. M. SHEN, An Inventory Location Model: Formulation, Solution Algorithm and Computational Results. Annals of Operations Research, vol. 110, 2002, pp. 83-106.
- DORIGO, M., L. M. GAMBARDELLA, Ant Colony System: a Cooperative Learning Approach to the Traveling Salesman Problem. Evolutionary Computation, IEEE Transactions on, vol. 1(1), 1997, pp. 53-66.
- DORIGO, M., L. M. GAMBARDELLA, Ant Colonies for the Travelling Salesman Problem. Biosystems, vol. 43(2), 1997, pp. 73-81.
- DORIGO, M., T. STÜTZLE, The Ant Colony Optimization Metaheuristic: Algorithms, Applications, and Advances. In Fred Glover and Gary A. Kochenberger, editors, Handbook of Metaheuristics, vol. 57, Springer US, 2003, pp. 250-285.
- DREZNER, Z., H. HAMACHER, Facility Location. Applications and Theory. Springer, Berlin, 2002.
- FIROOZI, Z., N. ISMAIL, S. ARIAFAR, S. H. TANG, M. K. A. M. ARIFFIN, A. MEMARINI, Distribution Network Design for Fixed Lifetime Perishable Products: A Model and Solution Approach. Journal of Applied Mathematics, vol. 2013. Article ID 891409
- GEOFFRION, A., R. ME BRIDE, Lagrangean Relaxation Applied to Capacitated Facility Location Problems. AIIE Trans., vol. 10(1), 1978, pp. 40-47.
- GHEZAVATI, V. R., M. S. JABALAMELI, A. MAKUI, A New Heuristic Method for Distribution Networks Considering Service Level Constraint and Coverage Radius. Expert Systems with Applications, vol. 36(3-1), 2009, pp. 5620-5629.
- HOLBERG, K., M. RONNQVIST, D. YUAN, An Exact Algorithm for the Capacitated Facility Location Problems with Single Sourcing. European Journal of Operational Research, vol. 113, 1999, pp. 544-599.
- KLINCEWICZ, J. G., H. LUSS, A Lagrangian Relaxation Heuristic for Capacitated Facility Location with Single-source Constraints. The Journal of the Operational Research Society, vol. 37(5), 1986, pp. 495-500.
- KUMAR, S. K., M. K.TIWARI, Supply Chain System Design Integrated with Risk Pooling. Computers & Industrial Engineering, vol. 64(2), 2013, pp. 580-588.
- MANIEZZO, V., L. M. GAMBARDELLA, F. DE LUIGI, Ant Colony Optimization. In Onwubolu and Babu, ed., New Optimization Techniques in Engineering, vol. 57, Springer-Verlag Berlin Heidelberg, 2004, pp. 101-117.
- MIRANDA, P. A., Un enfoque integrado para el diseño estrategico de redes de distribucion de carga. PhD thesis, Pontificia Universidad Catolica de Chile, 2004.
- MIRANDA, P. A., R. A. GARRIDO, Incorporating Inventory Control Decisions into a Strategic Distribution Network Design Model with Stochastic Demand. Transportation Research Part E, pp. Logistics and Transportation Review, vol. 40(3), 2004, pp. 183-207.
- MIRANDA, P. A., R. A. GARRIDO, Valid Inequalities for Lagrangian Relaxation in an Inventory Location Problem with Stochastic Capacity. Transportation Research Part E: Logistics and Transportation Review, vol. 44(1), 2008, pp. 47-65
- MIRANDA, P. A., R. A. GARRIDO, A Simultaneous Inventory Control and Facility Location Model with Stochastic Capacity Constraints. Networks and Spatial Economics, vol. 6, 2006, pp. 39-53.
- MOURITS, M., J. M. EVERS, Distribution Network Design: An Integrated Planning Support Framework. International Journal of Physical Distribution & Logistics Management, vol. 25, 1995, pp. 43-57.
- OSMAN, I. H., N. CHRISTOFIDES, Capacitated Clustering Problems by Hybrid Simulated Annealing and Tabu Search. International Transactions in Operational Research, vol. 1(3), 1994, pp. 317-336.
- OZSEN, L., C. R. COULLARD, M. S. DASKIN, Capacitated Warehouse Location Model with Risk Pooling. Naval Research Logistics, vol. 55(4), 2008, pp. 295-312.
- SHEN, Z. M., C. R. COULLARD, M. S. DASKIN, A Joint Location Inventory Model. Transportation Science, vol. 37(1), 2003, pp. 40-55.
- SIMCHI-LEVI, D., Y. ZHAO, The Value of Information Sharing in a Two Stage Supply Chain with Production Capacity Constraints. Naval Research Logistics, vol. 50(8), 2003, pp. 888-916.
- SIMCHI-LEVI, D., X. CHEN, J. BRAMEL, The Logic of Logistic. Springer-Verlag, New York, 2005.
- TANCREZ, J. S., J. C. LANGE, R. SEMAL, A Location Inventory Model for Large Three-level Supply Chains. Transportation Research Part E: Logistics and Transportation Review, vol. 48(2), 2012, pp. 485-502.
- JOHNSON, F., J. VEGA, G. CABRERA, E. CABRERA, Ant Colony System for a Problem in Reverse Logistic, Studies in Informatics and Control, vol. 24(2), 2015, pp. 133-140.
- TOADER, F. A. A Hybrid Algorithm for Job Shop Scheduling Problem, Studies in Informatics and Control, vol. 24 (2), 2015, pp. 171-180.
 Studies in Informatics and Control – ICI Bucharest
Studies in Informatics and Control – ICI Bucharest