R. J. VAZQUEZ GUERRA, J. F. MARQUEZ RUBIO,
B. del-MURO-CUÉLLAR, G. I. DUCHÉN SÁNCHEZ
Sección de Estudios de Posgrado e Investigación,
ESIME Unidad Culhuacán, Instituto Politécnico Nacional,
1000, Av. Santa Ana, Coyoacán, 04430, D. F. México
rjjvg@yahoo.com.mx, jfcomr23@yahoo.com.mx,
bdelmuro@yahoo.com, gduchen@ipn.mx

Abstract: In this work the problem of stabilization and control for recycling system is considered. Such class of systems is characterized by possessing two main paths named through this work as the direct (feedforward) and the recycling feedback) paths. This work considers recycling systems composed by a system of order n with one unstable pole at the direct path and a stable system of order m in the recycling path, both with different time delays. Two different dynamic delayed controllers are proposed in order to achieve a stable behavior of the closed-loop system. Stability conditions for the existence of these controllers are stated. The problems of step tracking and reject step disturbances are also addressed.

Keywords: Recycling system; Unstable processes; Time delay; Stabilization.

>>Full text>>
CITE THIS PAPER AS:
R. J. VAZQUEZ GUERRA, J. F. MARQUEZ RUBIO, B. del-MURO-CUÉLLAR, G. I. DUCHÉN SÁNCHEZ, Dynamic Delayed Controllers for Unstable Recycling Systems with Time Delays, Studies in Informatics and Control, ISSN 1220-1766, vol. 25(2), pp. 195-206, 2016. https://doi.org/10.24846/v25i2y201607

1. Introduction

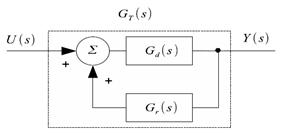
Recycling systems enable recovering energy and matter in a process. Such class of systems are commonly found in chemical industry for reducing the waste of reactants and hence, the cost of a reaction. Recycling systems are indeed closed loop feedback systems before being controlled. The term recycling is commonly used in process control literature in order to avoid confusion with single (not recycling) systems in closed loop (or feedback) with the controller. For instance a typical plant formed by reactor/separator process, where reactants are recycled back to the reactor [12,19]. Another example is a continuous stirred tank reactor (CSTR), where the output stream of the reactor is sent through a separation process, then, the unreacted reactants are returned into the CSTR through pipes. The presence of recycle streams introduces either positive or negative feedback structures into the system that can give rise to some undesirable effects [15]. An example of a recycling system is the recycle of the energy developed by an exothermic reaction in an adiabatic plug flow reactor for feed preheating. Instability could occur due to the exponential increase in the reaction rate with the temperature if it is not properly controlled [4]. Some works have studied the effects of the recycling systems, for instance, Luyben studied the effects of the recycle paths on dynamics process and their implications to plantwide control [10,11]. Scali and Ferrari discussed the robust control for recycling plants and proposed the concept of recycle compensation [16]. Similar approaches were extended by Lakshminarayanan and Takada [7], and Kwok et. Al [6]. In practice, it is quite common to ignore the recycle delay and use standard ordinary differential equation models. However, there has never been a theoretical explanation why this consideration is valid [9]. In fact, these references consider precisely simple ordinary differential equations for the analysis. It should be highlighted that the control problem becomes more complex when time delays in both, the direct and the recycling paths are present. In this situation, the transfer function of the total recycling system has a delay term in the numerator and additionally a second delay term in the characteristic equation. Then, the use of control structures for systems with a single time delay in the numerator, i.e., in the direct path, cannot be directly applied. For instance, the classical Smith Predictor deals with stable systems containing a single delay term in the transfer function. By another way, with an approach inspired in the Smith Predictor strategy, Márquez et. al¹⁴ have proposed a control methodology for recycling systems but restricted to unstable first order system at the direct path. This methodology is based on an estimated feedback taken from an observer-predictor.

This work considers the control problem of recycling systems composed by a system with n stable and one unstable poles at the direct path and m stable poles in the recycling path, both trajectories containing time delays. The key idea in our proposal is to use a delayed control feedback in order to establish the conditions to guarantee the closed loop stability. The idea of introducing a delay term into the controller has been previously used in the literature. For instance Abdallah et al. [1] consider a delayed term into controller for vibration mitigation. The dynamic delayed controllers here proposed do not only tackle a more general family of plants than the considered in Márquez et. Al [14], they are also easier to implement considering that this new proposal do not use any observer scheme to design the control law.