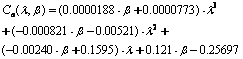Modelling and Power Regulation of Horizontal Variable Speed Wind Turbines
Andreea PINTEA
University “Politehnica” Bucharest
Splaiul Independentei 313, Bucharest, 60042, Romania
Haoping WANG
Nanjing University of Science and Technology, Automation School
Nanjing, China
Nicolai CHRISTOV
3 Lille University of Science and Technology
Villeneuve d’Ascq, 59651, France
Pierre BORNE
Ecole Centrale de Lille
59650, Villeneuve d’Ascq Cedex, France
Dumitru POPESCU
University “Politehnica” Bucharest
Splaiul Independentei 313, Bucharest, 60042, Romania
Abstract: This paper deals with the development of a nonlinear model of a horizontal variable speed wind turbine, the obtaining of an appropriate linear model and the design and analysis of a linear quadratic controller with disturbance estimation. The optimisation criteria will have to define an acceptable compromise between the limitations of the power level in the above rated wind speeds and the maintenance of the aerodynamic properties of the rotor at high solicitations exerted by the wind. The main control objective is to provide an amount of energy that will not exceed the nominal parameters of the generator thus avoiding overheating.
Keywords: Wind turbines, nonlinear systems, linear quadratic control.
>>Full text
CITE THIS PAPER AS:
Andreea PINTEA, Haoping WANG, Nicolai CHRISTOV, Pierre BORNE, Dumitru POPESCU, Modelling and Power Regulation of Horizontal Variable Speed Wind Turbines, Studies in Informatics and Control, ISSN 1220-1766, vol. 20 (3), pp. 305-312, 2011. https://doi.org/10.24846/v20i3y201111
1. Introduction
The last decades are characterized by an increase of the interest in the renewable energy sources and consequently in the need of finding control methods for optimizing the energy conversion. Among the renewable energy sources, the wind has become an attractive source of energy, determining in the same time the fastest growth of wind energy technology. Wind turbines are complex systems that function in a dynamic environment, where they risk being struck by lightning, or having ice deposed on the blades, stress, and even fire. But maybe the most important aspect is the variability of the wind. Different attempts to model this variation can be found in [1-3]. For our study though, we will consider the wind as constant in time and any change will be treated as a disturbance.
The studies done so far used either simplified either complex models of the wind turbine. But in most cases, the results concern only linear models [4-5], which are only approximations of the nonlinear models around a chosen functioning point [8]. This paper presents several preliminary results of a study aiming to provide a control solution for electric power limitation at high wind speeds where solicitations are extremely important and can provoke damages of the turbine’s structure. Because one needs prolonging the lifetime of the wind turbines components it becomes imperative in the control design to take into account the tower bending dynamics and the blade flexion modes. A disturbance observer based controller is proposed for estimating the external disturbances and then compensating them by using appropriate feedback. The controller performances are analyzed by numerical simulation for linear and nonlinear wind turbine models.
As it is well known there are many types of wind turbines configurations. From this variety, the ones operating at variable speed are currently the most used because of their numerous advantages. First of all, they are more flexible in terms of control and optimal operation [1], [9]. Secondly, the variable speed operation allows continuously adaptation of the rotational speed of the turbine in order to make the turbine operate constantly at its highest level of aerodynamic efficiency.
The performance of a wind turbine is characterized through its power coefficient Cp that depends in a nonlinear way of two parameters which are the tip speed ratio λ, and the pitch angle of the blades β [10-12]. The tip speed ratio represents the ratio between the tangential speed of the blade extremity
In this paper, Cp is calculated as
with ![]() and the coefficients c1 to c6 being: c1 = 0.18, c2 = 90, c3 = 115, c4 = 6.8, c5= 8 and c6 = 0.16. Its variation with respect to
and the coefficients c1 to c6 being: c1 = 0.18, c2 = 90, c3 = 115, c4 = 6.8, c5= 8 and c6 = 0.16. Its variation with respect to ![]() and
and![]() is given in Figure 1.
is given in Figure 1.
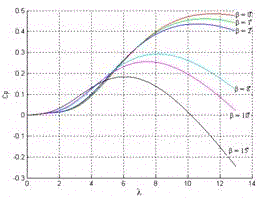
Figure 1. Power coefficient variation
The power coefficient,Cp, appears in the calculus of the aerodynamic torque Caero and the extracted power Paero:
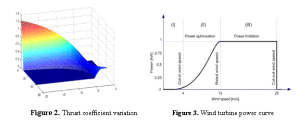
Another important coefficient of the turbine is the thrust coefficient Ca depending on the same two parameters, namely the tip speed ratio and the pitch angle, which define the thrust force Faero exerted by the wind on the rotor of the turbine [4-5]:
The thrust coefficient is defined as
and its variation with respect to λ and β is displayed in Figure 2.
A complex system can be easier studied if decomposed into subsystems, or its functioning regime is divided into several sub-regimes [6-7]. The wind turbine operation can be decomposed into three main operating zones depending on the speed of the wind. In Figure 3 one can find a typical power curve of a wind turbine.
The functioning regimes are: a) First Partial Load Area (I), b) Second Partial Load Area (II) and c) Full Load Area (III).
The first zone comprises wind speeds that vary up to approximately 4m/s. It is considered that bellow this value, the turbines consume much more energy that they manage to produce and in consequence they are not productive, therefore a turbine is started once wind surpasses this value of the wind speed.
In the second zone, (4-12m/s), the turbine starts gradually to produce energy, and to become efficient. The focus falls on the maximization of the extracted power. One tries to determine the turbine to function at a maximal value of Cp.
This value is also given by an optimal value of the tip-speed ratio λopt and of the pitch angle βopt. The preferred control technique in this region is the torque method which varies the torque developed by the generator, Cem, based on measurements of the tip speed ratio with keeping the pitch angle constant at βopt.
In the above rated wind speed (12-25m/s), also called high wind speeds area, the quantity of the electrical power delivered has to be limited to the nominal value of the generator in order to prevent its overheating. The most appealing control technique, called “pitch control” acts on the blades of the rotor, and it adjust them towards the feathered position, providing an effective control of the output power. The proposed control algorithm is designed for a wind turbine functioning in this regime.
References:
- NICHITA, C., D., Luca, B., Dakyo, E., Ceanga, Large band simulation of the wind speed for real time wind turbine simulators, IEEE Transactions on Energy Conversion, Vol.17, 2002.
- NICHITA, C., D., Luca, B., Dakyo, E., Ceanga, N. A., Cutululis, Modelling non stationary wind speed for renewable energy systems control, The Annals of “Dunarea de Jos” University of Galati, Fascicle III, 2000.
- LESCHER, F., P., Borne, Robust gain scheduling controller for pitch regulated variable speed wind turbine, Studies in Informatics and Control, Vol. 14, No. 4, 2005, pp. 299-315.
- LESCHER, F., J. Y., Zhao, P., Borne, Switching LPV controllers for a variable speed pitch regulated wind turbine, International Journal of Computers Communications and Control, Vol. 1, No. 4, 2006, pp. 75-86.
- WAFA, J., N., Bouguila, A., Khendher, State estimation via Observers with unknown inputs: application to a particular class of uncertain Takagi-Sugeno systems, Studies in Informatics and Control, Vol. 19, issue 3, pp. 219-228, 2010.
- MESAROVIC, M. D., D. Macko, Y., Takahara, Theory of Hierarchical, Multilevel Systems, Academic Press, New York, 1970.
- FILIP, F. G., K., Leiviska, Large scale complex systems, Springer Handbook of Automation, (S.Y. Nof, Ed.), pp 619-638, Springer, Dordrecht, 2009.
- KLEMPNER, G., I., Kerszenbaum, Operation and maintenance of large turbo-generators, Wiley Interscience, A John Wiley & Sons, Inc, Hoboken, New Jersey, USA, 2004.
- BURTON, T., D., Sharpe, N., Jenkins, E., Bossanyi, Wind energy handbook, Wiley &Sons, Chichester, 2002.
- HAU, E., Wind turbines, fundamentals, technologies, and applications in economics, 2nd edition, Springer-Verlag, Berlin, 2006, p. 103.
- MUNTEANU, I., A., I., Bratcu, N., A., Cutululis, E., Ceanga, Optimal control of wind energy systems – Towards a global approach, Springer-Verlag, London, 2008.
- LIM, C.W., K. Y., Seo, A comparative study on responses in the optimal region according to torque control methods for wind turbines, Proceedings of the International Conference on Control Automation and Systems, Kintex, Gyeonggi-do, Korea, 2010, pp. 1066-1072.
- KASPER, Z. O., Robust gain scheduled control of wind turbines, Phd Thesis, Automation and Control Department of Electronic Systems, Aalborg University, Denmark, 2008.
- ARCZEWSKY, K., W., Blajer, J., Fraczek, M., Wojtyra, Multi-body dynamics, Computational methods in applied sciences, Springer Verlag, Dordrecht, 2010.
- JAIN, P., Wind energy engineering, McGrawHill, New York, 2011.
- SPERA, D., A., Wind turbine technology, fundamental concepts of wind turbine engineering, 2nd Edition, Asme Press, New York, 2009.
- KUTZ, M., Mechanical Engineers’ Handbook, Materials and Mechanical design, John Wiley & Sons, Inc., New York, 2006.
- BIANCHI, F., H., Battista, R., Mantz, Wind turbine control systems – Principles, modeling, and gain scheduling design, Springer-Verlag, Berlin, 2007.
- MITA, T., M., Hirata, K., Murata, H., Zhang, H∞ control versus Disturbance Observer based Control, IEEE Transactions onIndustr. Electronics, Vol. 45, June, 1998, pp. 488-495.
- CHEN, W., H., Disturbance observer based control for nonlinear systems, IEEE/ASME Transactions on mechatronics, Vol. 9, No. 4, Dec., 2004, pp. 706-711.
- SIMON, D., Optimal state estimation – Kalman, H∞, and nonlinear approaches, Wiley Interscience, Hoboken, New Jersey, 2006.
- ZHOU, K., Doyle J., Glover K., Robust and optimal control, Prentice Hall, Englewood Cliffs, 1995.
 Studies in Informatics and Control – ICI Bucharest
Studies in Informatics and Control – ICI Bucharest