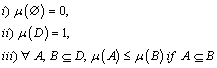A Model to Support Risk Management Decision-Making
Ayeley Philippe TCHANGANI
Université de Toulouse, Université Toulouse III – IUT de Tarbes
1 rue Lautréamont, 65016 Tarbes Cedex, France
Université de Toulouse, Laboratoire Génie de Production – ENIT
47 Avenue d’Azereix, 65016 Tarbes Cedex, France
Abstract: This paper considers the issue of designing a framework to efficiently manage the risk due to some adverse events an organization or a system may face. Risk comes from human being’s incapacity to predict the consequences or outcomes of some external events and/or their own actions, or to express precisely their knowledge about things. Thus, risk is linked to uncertainties that are inherent to almost all activities of human being. Designing an effective risk management decision making framework necessitate to correctly address these uncertainties in terms of appropriate mathematical tools along with procedures to identify variables (risk factors, state of the system, consequences, objectives or stakes, possible actions, etc.) impacting decision process and relationships linking them and finally aggregating approaches to present high level managers with concise information. In this paper we will use a meta-matrix analysis to identify relationships between previously determined variables, Bayesian networks and influence diagrams, graphical tools that permit easy representation of probabilistic relationships (independence, causality, correlation, etc.) between variables to quantify these relationships, and Choquet integral as an aggregation tool.
Keywords: Risk assessment and management, meta-matrix, Bayesian networks, influence diagrams, fuzzy integral.
>>Full text
CITE THIS PAPER AS:
Ayeley Philippe TCHANGANI, A Model to Support Risk Management Decision-Making, Studies in Informatics and Control, ISSN 1220-1766, vol. 20 (3), pp. 209-220, 2011. https://doi.org/10.24846/v20i3y201102
1. Introduction and Statement
1.1. Introduction
Facing an adverse event (an earthquake, a hurricane, a malicious action, the failure of a machine, etc.), managers of an entity (a physical system, a human organization, etc.) will be concerned with the impact on their objectives or stakes that we will generically refer to as their desires in this paper. These desires are the main issues that will guide actions which managers may consider in order to reduce as much as possible the negative impact of the event. But the outcomes of these actions are always subject to uncertainty creating then a risky situation. So risk can be defined as the uncertainty of the consequences or outcomes of events and/or actions. To correctly address uncertainties mainly in terms of mathematical tools to represent them, we need to know their nature.
Roughly, there are three types of uncertainties briefly explained below.
Epistemic uncertainty: this type of uncertainty is due to incomplete knowledge and it ranges from deterministic knowledge to complete total ignorance; for instance the question “are genetically modified organisms dangerous for human being?” is subjected to epistemic uncertainty. Epistemic uncertainty can be reduced or transformed to variability uncertainty provided that the analyst or decision maker disposes of time and/or resources to do studies or to observe the system; decision making problems where this type of uncertainty also known as severe uncertainty occurs are generally solved by worst case analysis or Wald’s maxi/min principle [23]; we are not going to address this kind of uncertainty in this paper.
Variability uncertainty is due to the inherent variability in the behaviour of some components of a decision making problem (environment, humans, outcomes, etc.). The uncertainty related to a question such as “what will be the magnitude of the next earthquake in Japan?” can be considered to be subjected to variability uncertainty. Contrary to epistemic uncertainty, variability uncertainty is not reducible and must be adequately addressed by mathematical tool in any rational decision making problem. The appropriate mathematical tool to manage variability uncertainty is the theory of probability and its connected graphical tools such as Bayesian networks and influence diagrams [9, 14].
Fuzzy uncertainty: this uncertainty comes mainly from the impossibility of humans to precisely define events or variables and/or the fuzzy discretization of continuous variables. Indeed, humans usually express their opinions in terms of linguistic variables such as: this is a tall person, this season we expect our sale to be high, etc. The mathematical tool to address fuzzy uncertainty is naturally the fuzzy set theory (see [21]).
In this paper we will be concerned by variability and fuzzy uncertainties.
Integration of risk factors in decision making or risk informed decision making is receiving a great attention by researchers and decision makers in many domains such as engineering (designing technical systems that mitt some requirements in terms of safety), finance (set up norms to monitor finance activities in order to avoid companies collapse), environment (develop sustainable agriculture and natural resources extraction actions), science and medical research (monitoring scientists activity by the society to avoid creating new threats) because national and international opinions are being more and more sensible to risk issues from all human activities. The purpose of this paper is to develop a risk management framework and a generic model that can be used to support making and planning pre-active, reactive or proactive decisions.
Pre-active decisions: these decisions consist in doing things to prepare the entity under consideration to face potential adverse events (one knows that such events will occur soon or later). Actions such as transferring risk by contracting insurances, editing anti-seismic construction norms in the case of natural disasters or prudential norms such as those of Bâle II (see for instance [22]) concerning banking activities, preparing population on how to behave in the case of an earthquake, constructing and organizing emergency facilities, etc. are pre-active decisions.
Reactive decisions: reactive decisions consist in real time actions when the adversary events are present; decide which emergency unit will be affected to which zone or region during an earthquake; which credit to reduce by a government when an unplanned event such as petrol price raise occurs, renegotiating contracts with partners when they fail to realize their duties or redirecting activities in a supply chain for instance, etc. constitute reactive decisions.
Pro-active decisions: they consist in things that must be undertaken to force a particular situation (avoiding catastrophic situation for instance). Risk prevention using redundancy for instance (to avoid the failure of a function or component in an industrial system), destroying or weakening terrorist groups such as Al Quaida by military actions in order to prevent events like that of 9/11 participate to such proactive decisions.
Risk and uncertainty are fundamental elements of modern life so they must be managed effectively to protect people from injury and to permit the development of reliable, high-quality products. Today an ever-increasing number of professionals and managers in industry, government, and academia are devoting a larger portion of their time and resources to the task of improving their approach to, and understanding of, risk-based decision making [7, 10]. Indeed, decision making under uncertainty (risk) literally encompasses every facet, dimension, and aspect of our lives. Any decision maker needs to cope with uncertainty in order to rationally act in the sense of risks reduction. To correctly and scientifically address risk management process, one needs a precise definition and measure of risk; this is the object of next paragraph.
1.2. Risk definition and measure
Risk is jointly associated with the likelihood (probability) of something (an event or a sequence of events) happening and the negative impact (severity) on the entity which arises if it does actually happen. As stated previously the impact will be considered with regard to the entity managers desires. So to formerly define the risk, let us consider that when facing an adverse event X entity managers have identified a finite discrete set D of desires. The measure Rd(X) of the risk for a desire d with regard to an adverse event X is consequently formed by two components: the likelihood Pr(X) of the event X (probability of occurrence) and the severity Sd(X) (a conditional measure of the extent to which the desire d will not be satisfied if event X actually happens). The severity depends on the entity state that is all things that make it being vulnerable or resilient with regards to the adverse event. These components are such that if one of them is given, the risk is commensurate to the another and there is no risk if one of them is null; indeed, if an event is almost impossible (Pr(X) ≈ 0)) it does not matter if its severity is high or not and a highly probable event does not matter if its severity can be neglected (Sd(X) ≈ 0). Thus the measure Rd(X) of the risk on desire d with regard to event X is given by equation (1) below.
The severity measures conditional negative impact on the desire and generally expressed by the amount of some losses (economic loss, lives loss, etc.) or by the probability of it being not satisfied; desire that may be formulated as a constraint on some consequences of. When severity is considered to be the conditional probability of no satisfaction of desire knowing the event X, that is ![]() is given by equation (2).
is given by equation (2).
the risk corresponds to the joint probability of the occurrence of event X and non satisfaction of desire d, that is ![]() will be reduced to equation (3).
will be reduced to equation (3).
The global risk R(X) for the entity given the event X will be obtained by aggregating risks related to all desires as shown by equation (4) below.
![]() (4)
(4)
where ![]() is an aggregating operator over the desires set D.
is an aggregating operator over the desires set D.
Many approaches, see [4], exist to construct aggregation operator ![]() ranging from simple weighted sum to more sophisticated approach that take into account some interaction between measures to aggregate, see [5]. One such approach known to cope with synergy (when some measures are complementary) between measures, redundancy (the case where some measures are substitutable) and independency between measures is the Choquet integral [3]. The following definition gives necessary materials to compute this overall risk as a Choquet integral.
ranging from simple weighted sum to more sophisticated approach that take into account some interaction between measures to aggregate, see [5]. One such approach known to cope with synergy (when some measures are complementary) between measures, redundancy (the case where some measures are substitutable) and independency between measures is the Choquet integral [3]. The following definition gives necessary materials to compute this overall risk as a Choquet integral.
Definition: Let ![]() be the power set of D, a function
be the power set of D, a function ![]() is a capacity or a fuzzy measure over D if it verifies:
is a capacity or a fuzzy measure over D if it verifies:
Given a capacity ![]() over the set of desires D, the global risk R(X) is given by the Choquet integral associated to this capacity as given by the following equation (6)
over the set of desires D, the global risk R(X) is given by the Choquet integral associated to this capacity as given by the following equation (6)
![]() (6)
(6)
where ![]() is the cardinality of the set D,
is the cardinality of the set D, ![]() is a permutation over D such that
is a permutation over D such that
The difficulty of computing Choquet integral is to define a fuzzy measure over the set D that necessitates obtaining ![]() coefficients that represent the measure of subsets of D other than
coefficients that represent the measure of subsets of D other than ![]() and D. This can be done by experts if the set D is not too large otherwise, by some practical considerations, such as k-additive fuzzy measure, one can obtain this integral with less computational effort through interaction indices for instance [5].
and D. This can be done by experts if the set D is not too large otherwise, by some practical considerations, such as k-additive fuzzy measure, one can obtain this integral with less computational effort through interaction indices for instance [5].
Now that risk and its measure are defined, we consider the way to manage it. The process of coping with risks in running an entity is twofold: be aware of what kind of risks the entity can face (risk assessment) and what can be done to reduce the overall impact of those risks (risk management); these two issues will be considered in the following paragraph.
1.3. Risk assessment and management
Assessment process is a purely analytic activity where the analyst is willing to characterize the risks faced by an entity by following some procedures. In risk assessment, the analyst often attempts to answer the following set of triple questions.
What can go wrong? Answers to this question will permit to identify all events or sequence of events (or scenarios) that have an (negative) effect on the entity.
What is the likelihood that it would go wrong? This is the quantification process to estimate probability of occurrence of formerly identified risk factors or events.
And, what are the consequences? Answers to this question permit to identify and estimate the possible negative impact on the entity (complete failure of a system, approximate running of a system, serious disorganization of an organization, dangerous situation for users, etc.) if the undesired events do occur. These consequences result from the events as well as the state of the entity; the state of an entity here consists in all things (cognitive, physical, organizational, architectural, sensitivity, adaptive capacity, etc.) that make it vulnerable or in contrary resilient to undesirable events.
Answers to these triple questions help risk analysts identify, measure, quantify, and evaluate risks and their consequences and categorize the risk factors (adverse events). In general the categorization of risk factor is done as given on Figure 1 where we have: critical events (either frequent and severe events), these events must be seriously monitored; frequent but not severe events (one may consider reducing their frequency by improving the technology of related components in a system for instance); severe but not frequent events (one may consider actions that prevent their impact by organizing the architecture of the system to tolerate related faults); not critical events (not frequent nor severe events, no real danger concerning these events)
Formalized tools such as that developed in dependability engineering namely, FMECA (Failures Modes, their Effects and Criticity Analysis), fault tree analysis, reliability diagrams and many other specialized approaches, see for instance [1, 4, 17, 18, 19], can be useful for risk assessment purpose.
 Figure 1. Risk factors categorization and risk management actions typology
Figure 1. Risk factors categorization and risk management actions typology
If being aware of risks that an entity is facing (risk assessment) is a necessary non avoidable condition, being able to act to reduce this risk (risk management, acting in the sense of arrows shown on Figure 1, rendering all events not critical) is probably the better thing to do; in the following paragraph risk management process will be formulated.
Risk management is decision making under uncertainty using quantified measure of the later [16] and its objective is to investigate the trade-off between the conveniences and the consequences. Risk management builds on the risk assessment process by seeking answers to a second set of three questions:
What can be done and what options are available? The answer to this question permit to identify a finite discrete set A of possible actions that can be undertaken to either mitigate the risk (reducing the severity) or to prevent the risk (reducing the likelihood) or both of them. Notice that depending on the nature of the events some of these actions may be impossible; for instance it is not possible to prevent a natural risk such as an earthquake; these risks can be just mitigated by taking appropriate actions such as respecting seismic norms when constructing infrastructures and buildings and/or preparing population to have good reflex when necessary.
What are the associated trade-offs, in terms of all costs and benefits and constraints in the realization of actions identified in the previous point?
And what are the impacts of the undertaken management actions on future options.
In the next section, we will expose the framework we are proposing to support risk management decision making process.
References:
- AVEN, T., Reliability and Risk Analysis, 1st Ed. Elsevier Applied Science, 1992.
- BAYES, T., Towards Solving a Problem in the Doctrine of Chances, Biometrica (46), 1958, pp. 293-298 (reprinted from an original paper of 1763).
- GRABISCH, M., Fuzzy Integral in Multicriteria Decision Making, Fuzzy Sets & Systems 69, 1995, pp. 279-298.
- GRABISCH, M., The Application of Fuzzy Integrals in Multicriteria Decision Making, European J. of Operational Research 89, 1996, pp. 445-456.
- GRABISCH, M., K-Order Additive Discrete Fuzzy Measures and Their Representation, Fuzzy Sets & Systems 92, 1997, pp. 167-189.
- HOWARD, R. A., MATHESON, J. E., Influence Diagrams, in The principles and Applications of Decision Analysis, R. A. Howard and J.E. Matheson (Eds) (2), 1984, pp. 719-762.
- HM TREASURY, The Orange Book. Management of Risk – Principles and Concepts, Crown, 2004.
- Hugin Expert, http://www.hugin.com/
- JENSEN, F. V., Bayesian Networks and Decision Graphs, Springer, 2001.
- MAGNE, L., D. VASSEUR, Risques Industriels. Complexité, Incertitude et Decision: une approche interdisciplinaire, (in french), Lavoisier, 2006.
- MURPHY, K. P., Dynamic Bayesian Networks: Representation, Inference and Learning, Ph.D. Thesis, University of California, Berkeley, 2002.
- NAÏM, P., P.-H. WUILLEMIN, P. LERAY, O. POURRET, A. BECKER, Réseaux bayésiens (in french), Eyrolles, 2004.
- Netica, http://www.norsys.com/
- PEARL, J., Probabilistic Reasoning in Intelligent Systems, Morgan Kaufmann, 1988.
- SMETS, P., KENNES, R., The Transferable Belief Model, Artificial Intelligence, vol. 66, 1994, pp. 191-243.
- SINGPURWALLA, N. D., Reliability and Risk: A Bayesian Perspective, John Wiley & Sons, 2006.
- STAMATIS, D. H., Failure Mode and Effect Analysis – FMEA from Theory to Execution, ASQC Quality press, 1995.
- SUTTON, I. S., Process Reliability and Risk Management, 1st Ed. Van Nostrand Reinhold, 1992.
- TCHANGANI, A. P., Reliability Analysis using Bayesian Networks, Studies in Informatics & Control Journal vol. 10(3), 2001, pp. 181-188.
- TCHANGANI, A. P., D. Noyes, Modelling Dynamic Reliability using Dynamic Bayesian Networks, European Journal of Automation, vol. 40(8), 2006, pp. 911-935.
- TERANO, T., K. ASAI, M. SUGENO, Fuzzy Systems Theory and Its Applications, Academic Press, 1987.
- THORAVAL, P.-Y., Le dispositif de Bâle II: rôle et mise en oeuvre du pilier 2, Revue de la stabilité financi&egarve;re (9), Banque de France, 2006, pp. 125-132, (in french).
- WALD, A., Statistical Decision Functions, New York: Wiley, 1950.
- Working Group Macroseismic Scales, European Macroseismic Scale 1998 EMS-98, Cahiers du Centre Européen du Géodynamique et de Sismologie (15), Edition Conseil de l’Europe, 1998.
 Studies in Informatics and Control – ICI Bucharest
Studies in Informatics and Control – ICI Bucharest