Pattern Formation and Stability Issues in Coupled Fuzzy Map Lattices
Horia-Nicolai TEODORESCU
Gheorghe Asachi Technical University of Iasi, Institute of Computer Science of the Romanian Academy
11, Carol I, Iasi, Romania 2, Codrescu, 700481, Iasi, Romania
Abstract: The aim of the paper is to investigate stability issues and mechanisms of pattern formation in coupled map lattices (CMLs) that use fuzzy nodes. The lattices belong to various topologies, including rings with various vicinities, and linear topologies. The use of fuzzy maps instead of deterministic (crisp) maps in coupled map lattices improves the modelling capabilities and enhances the ability to model complex systems, making CMLs particularly useful for applications where we face uncertainty and imprecision. One of the questions we answer relates to the computational requirements for determining that a periodic pattern of period p develops in a CfML.
Keywords: Nonlinear dynamics, modelling, fuzzy logic, Lyapunov exponent, patterns.
>>Full text
CITE THIS PAPER AS:
Horia-Nicolai TEODORESCU, Pattern Formation and Stability Issues in Coupled Fuzzy Map Lattices, Studies in Informatics and Control, ISSN 1220-1766, vol. 20 (4), pp. 345-354, 2011. ttps://doi.org/10.24846/v20i4y201102
1. Introduction
Coupled Map Lattices (CMLs), also named Coupled Map Networks (CMNs), represent a well-established tool in modeling diffusion and flow processes. CMLs are currently used to represent models of such various processes as laminar and turbulent flows, heat propagation, biological population dynamics, and economic processes [8, 11-13, 20-22].
Typical CMLs operating in discrete time are represented by systems of discrete recursive equations with variables with at least two indices, characterized by some form of regular relationship between the variables with indices with close values. The regularity is due to the fact that the nodes in the lattice operate according to influences coming from neighboring nodes, where the neighborhoods are similar [10,12,27], as in Figure 1. The general equation of a node is written as
xi,t=ƒ(xhi,t-1), (1)
Where xi,t is the output of the node with the corresponding indices, ƒ stands for the input-output function of the node and the variable xh is a vector representing the outputs of the nodes in the vicinity of the node i, at previous time moment,
xhit=(xi-h,t,xi-h+1,t,…,xi,t,…,xi+h,t). (2)
In Equations (1) and (2), the index i stands for the position of the node in the row. When the rows are finite, i=1,?,N. The index t stands for the time moment; one row in the lattice is assigned to each time moment, t=0,…,∞, or t=0,…,M for finite evolutions.
The value 2h+1=ct represents the number of cells (nodes) in the vicinity. The vicinity is assumed symmetrical in (2). A set of initial conditions are needed to solve the equations (1) and (2). The initial conditions represent the values of the variables with the second index 0, xi,0; these values are assumed known. The number of indices can be extended at will for creating planar and spatial lattices; for example, two indices can be used to denote space, and the third index is used to denote time.
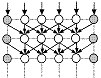
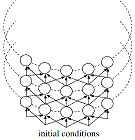
Figure 1. (a) Semi-planar coupled map lattice with finite rows; the shaded nodes have boundary condition values. (b) An annular lattice.
The set of equations (1) and (2) can be supplemented with boundary conditions when the lattice is linear and the rows in the lattice have a finite number of nodes. The boundary conditions are either prescribed or reproduce the values of the corresponding boundary nodes on the first row. A CML without boundary conditions is named freely evolving or isolated CML. The boundary conditions refer to constraints imposed to some of the values of the variables, typically to the predetermined values of the “extreme” (boundary) cells, x1j=aj, xNj=bj.
A simple case of CML uses weighted linear combinations of the outputs of the neighbors, as in multilayer neural networks. Symmetric wi+k=wi-k and antisymmetric wi+k=-wi-k couplings are frequently used [23]. In all the above CMLs, the neighborhood includes elements on both sides, like in Figure 1. This type is named diffusion-type CML. In contrast, if the neighborhood includes only elements on one side, the CML is said to have one-way coupling. These networks are also named uni-directionally coupled map lattices. In case of one-way coupling, a CML with linear nodes has the equation
Time-delayed map are defined by equations involving time lags larger than 1, as [23],
There are alternative ways of describing CMLs based on graphs. Assume a lattice-type oriented graph. The orientation is interpreted as (time-) propagation. To each node of the graph, attach vicinities (all similar) and a characteristic function. With initial condition for the first line and boundary conditions, we propagate from the first line.
The CML is asymptotically stable when the states of the lines converge when time goes to infinity. When the convergence occurs in a finite number of lines, the behavior is stable. The CML may be periodical, with the states of the lines repeating periodically. CMLS with nonlinear nodes-depending on the initial conditions- may evolve chaotically.
For a process to have a CML model, several conditions have to be fulfilled. In the first place, the process has to have similar components that can be modeled with identical cells, or with a small set of different cells. In the second place, the elements in the process should have a spatial distribution that is regular and corresponds to a simple graph, as a line graph, a circular graph (loop), or a planar regular graph. While more complex graphs have been proposed, computations are easier on simple graphs. Third, the connections between the elements, which model how one element influences the others, should fall in the category of models based on vicinities. Examples of processes that obey these conditions are the atom movements in a crystal, the spins in a magnetic material, the cars on a one-way road, and people sitting in a stadium. To such processes, simple graphs can be attached and a description of the process with a CML is easily done. More examples are introduced in the next section of the paper.
The CMLs described above are deterministic, because the characteristic functions of their nodes were tacitly assumed deterministic ones. CMLs with probabilities are also well-know in physics as models of magnetic and diffusion processes [5, 9, 23].
A generalization of the CMLs, using fuzzy logic systems for describing the behavior of the nodes (cells) in the CML, was introduced in [25, 26]. The use of fuzzy logic in conjunction with CMLs has several reasons, including the need to simulate networks of human decision makers and the need to deal with dynamic pattern formation and pattern recognition in processes well described by fuzzy logic, as speech [19] and biological signals [30, 31]. There are two cases of CMLs with fuzzy logic cells. In the first, the cells are modeled by FLSs with defuzzification; the second uses nodes modeled by FLSs with fuzzy outputs (no defuzzification at the output).
In Section 2, we present the notion of coupled fuzzy maps and provide the basic equations and examples of applicability. In Section 3, we discuss issues related to pattern formation in crisp and fuzzy CMLs. The last section concludes the paper.
Notations: Throughout this paper, xtk and xk,t denote a variable related to the kth cell of the row, at time moment t. The variable x is used in general for the input and output of cells, the notation u is used for aggregation of input variables, and ƒ(.) denotes the function describing the cell. Whenever the time moment is obvious, we may drop the t index. The symbol μ is reserved for membership functions (m.f.) and β for output singletons in a Sugeno-type FLS. CfML stands for Coupled fuzzy-Map Lattice, fCML stands for fuzzy-Coupled Map Lattice, while FLS stands for Fuzzy Logic System.
REFERENCES:
- ADRIAENSSENS, V., B. DE BAETS, P. GOETHALS, N. DE PAUW, Fuzzy Rule-Based Models for Decision Support In Ecosystem Management. Science of the Total Environment, Vol. 319, (1-3), 2004, pp. 1-12.
- AMRITKAR, R. E., J. SARIKA, H., CHIN-KUN, Synchronized Clusters in Coupled Map Networks. II. Stability Analysis Physical Review E, Vol. 72, 1, 016212_1-016212_9, 2005.
- AMRITKAR, R. E., J. SARIKA, H., CHIN-KUN, Synchronized Clusters in Coupled Map Networks. II. Stability Analysis. Physical Review E Vol. 72, 016212, 016212-1 — 016212-9, 2005.
- ATAY, F. M., O. KARABACAK, Stability of Coupled Map Networks with Delays, SIAM J. Appl. Dyn. Syst., Vol. 5, 3, 2006, pp. 508-527.
- DE AGUIAR, M. A. M., I. R. EPSTEIN, Y. BAR-YAM, Analytically Solvable Model of Probabilistic Network Dynamics, Physical Review E, 772, 067102, 067102-1- 067102-4, 2003
- DUBOIS, D., H. FARGIER, H. PRADE, P. PERNY, Qualitative Decision Theory: from Savage’s Axioms to Nonmonotonic Reasoning. Journal of the ACM (JACM), Vol. 49, 4, 2002, pp. 455-495.
- ATAY, F. M., J. JOST, A. WENDE, Delays, Connection Topology, and Synchronization of Coupled Chaotic Maps. Phys. Rev. Let., 92, 144101, 2004.
- GALLUCIO, A., New Algorithm for the Ising Problem: Partition Function for Finite Lattice Graphs, Physical Review Letters, Vol. 84, 26, 2000, pp. 5924-59277.
- GHEORGHIU-SVIRSCHEVSKI, S., Y. BAR-YAM, Multiscale Analysis of Information Correlations in an Infinite-Range, Ferromagnetic Ising System, Phys. Rev. E, Vol. 70, 6, 066115, 2004
- JIANG M., Q. ZHANG, A Coupled Map Lattice Model of Tree Migration. Discrete Contin. Dyn. Syst. B, Vol. 9, 1, 2008, pp. 83-101.
- KADJI, E., J. C. OROU, P. WOAFO, Spatiotemporal Dynamics in a Ring of N Mutually Coupled Self-Sustained Systems. Chaos, Vol. 17, 033109, 2007
- KANEKO, K., Simulating Physics with Coupled Map Lattice. Formation, Dynamics and Statistics of Patterns 1, World Scientific, Singapore, 1990.
- KANEKO, K., Overview of Coupled Map Lattices. Chaos, Vol. 2, 3, 1992., pp. 279-282
- LEE, C. C., Fuzzy Logic in Control Systems: Fuzzy Logic Controller, Part II, IEEE Trans. Systems, Man, Cybernetics, Vol. 20, 2, 1990, pp. 419-435.
- LI X., G. CHEN, Synchronization and Desynchronization of Complex Dynamical Networks: An Engineering Viewpoint. IEEE Trans. Circuits and Systems-I: Fundamental Theory and Applications, Vol. 50, 11, 2003, pp. 1381-1390
- MANRUBIA, S. C., A. S. MIKHAILOV, Mutual Synchronization and Clustering in Randomly Coupled Chaotic Dynamical Networks. Physical Review E, Vol. 60, 1999, pp. 1579-1589.
- MANRUBIA, S. C., A. S. MIKHAILOV, Very Long Transients in Globally Coupled Maps. Europhysics Letters, Vol. 50, 2000, pp. 580-586
- RESTEANU C., R. TRANDAFIR, Programming Problems with a Large Number of Objective Functions. Dimov I, Dimov S, Kolkovska N. (Eds.), Numerical Methods and Appl., Lecture Notes Comp. Sci., Vol. 6046, 2011, pp. 207-214.
- RODRIGUEZ, W., H. N. TEODORESCU, F. GRIGORAS, A. KANDEL, H. BUNKE, A Fuzzy Information Space Approach to Speech Signal Non-linear Analysis. Int. J. Intelligent Syst. Vol. 15, 4, 2000, pp. 343-363
- RUDZICK O., PIKOVSKY, A., Unidirectionally Coupled Map Lattice as a Model for Open Flow Systems. Physical Review E Vol. 54, 5, 1996, pp. 5107- 5115.
- SAYAMA, H., L. KAUFMAN & BAR-YAM, Spontaneous Pattern Formation and Diversity in Spatially Structured Evolutionary Ecology, In: Focus on Biodiversity Research, J. Schwartz (Ed.), 1-16, Nova Science Publishers, Inc., 2006
- SEKI M., K. ITO, A Coupled Map Lattice for Geomagnetic Polarity Reversals That Exhibits Realistic Scaling, Earth Planets Space, Vol. 51, 1999, pp. 395-902.
- SPROTT, J. C., G. ROWLANDS, Chaos Demonstrations. User’s Manual. American Institute of Physics, N.Y., 1995
- SCHUMANN, A. W., Q.U. ZAMAN, Software Development for Real-Time Ultrasonic Mapping of Tree Canopy Size. Comp. & Electr. Agric., vol. 47, 2005, pp. 25-40.
- TEODORESCU H. N., Coupled Map Networks and Uncertainty propagation. Int. J. Chaos Theory & Appl., Vol. 8, 1, 2002, pp. 3-16.
- TEODORESCUH. N., Self-organizing Uncertainty-based Networks. 131-160. In: P. Melo-Pinto, H.-N. Teodorescu and T. Fukuda (Eds.), Systematic Organisation of Information in Fuzzy Systems, NATO Sci. Series III, Vol. 184, 2003, pp. 131-159.
- TEODORESCU H. N., Information, Data, and Information Aggregation in Relation to the User Model. In Melo-Pinto P., Teodorescu HN., Fukuda T, (Eds.), Systematic Organisation of Information in Fuzzy Systems, NATO Sci. Series III, vol. 184, 2003, pp. 7-10.
- TEODORESCU H. N., Parallelizing Dynamic Models Based on Fuzzy Coupled Map Networks. Proc. 4th IEEE Int. W. Intell. Data Acquisition & Adv. Comp. Systems, Dortmund, Sept. 06-08, 2007, pp. 170-175.
- TEODORESCU H. N., On Fuzzy Sequences, Fixed Points and Periodicity in Iterated Fuzzy Maps. Int. J. Comp., Comm. & Control, Vol. 6, 4, 2011, pp. 748-759.
- TEODORESCU H. N., A. KANDEL, M. SCHNEIDER, Fuzzy Modeling and Dynamics. Fuzzy Sets and Systems, Vol. 106, 1, Aug. 16, 1999, pp. 1-2.
- TEODORESCU H. N., A. KANDEL, L. HALL, Report of Research Activities in Fuzzy AI and Medicine at USFCSE. AI in Medicine, Vol. 21, 1-3, 2001, pp. 177-183.
- TEODORESCU H. M., M. D. ZBANCIOC, L. PISTOL, Parallelizing Neuro-fuzzy Economic Models in a GRID Environment, Studies in Informatics and Control, Vol. 17, 1, 2008.
- ZADEH, L. A., Fuzzy Logic = Computing with Words. IEEE Trans. Fuzzy Systems, Vol. 4, 2, 1996, pp. 103-111.
 Studies in Informatics and Control – ICI Bucharest
Studies in Informatics and Control – ICI Bucharest