Friday , April 26 2024

Solving a Distribution Network Design Problem
by means of Evolutionary Algorithms

Guillermo CABRERA1, Stefanie NIKLANDER2,3, Enrique CABRERA4, Franklin JOHNSON5

1 Pontificia Universidad Católica de Valparaíso, Chile
guillermo.cabrera@ucv.cl
2 Universidad Autónoma de Chile, Chile
3 Universidad Científica del Sur, Peru
sniklander@gmail.com

4 Universidad de Valparaíso, CIMFAV, Chile
enrique.cabrera@uv.cl
5 Universidad de Playa Ancha, Chile
franklin.johnson@upla.cl

Abstract: In this paper a simple and efficient evolutionary algorithm is implemented to solve a Distribution Network Design problem (DND). The DND problem that we address here integrates inventory policies with location/allocation decision making. This problem, also known as Inventory Location Modeling problem, is a complex combinatorial optimization problem that cannot be solved by exact methods as the number of decision variables increases. We compare our algorithm to previously implemented algorithms. Our evolutionary approach is shown to be very competitive in terms of both objective function value and execution time.

Keywords: Evolutionary Algorithm, Distribution Network Design, Logistics, Combinatorial Optimisation.

>>Full text<<
 CITE THIS PAPER AS:
Guillermo CABRERA, Stefanie NIKLANDER, Enrique CABRERA, Franklin JOHNSON, Solving a Distribution Network Design Problem by means of Evolutionary Algorithms, Studies in Informatics and Control, ISSN 1220-1766, vol. 25(1), pp. 21-28, 2016. https://doi.org/10.24846/v25i1y201603

  1. Introduction

The problem of locating/allocating customer to distribution centres is one of the most studied problems in logistics. Usually, after decision makers determine the locations to be installed, the inventory policy is defined. However, this sequential approach is sub-optimal in the sense that the inventory policy is restricted by the network design determined in the previous step. Thus, integrating location/allocation decisions and inventory policies lead to solutions that are more efficient as they consider the entire system as a whole.

On the one hand, the location/allocation problem consists of selecting specific sites at which to install plants, warehouses and/or distribution centres while assigning customers to service facilities and interconnecting facilities using flow assignment decisions [6, 10].

On the other hand, inventory policies determine tactical issues such as reorder point and order size, among others.

Figure 1 shows a schema of both the sequential and the integrated approaches. On the left hand side, the sequential approach is presented. As we can see, the first decision to be made is the location-allocation one. Once this decision is made, we can go to the next step which is to decide among the different inventory policies that are able to be implemented. Once this tactical decision is made, other operational issues are addressed. No change on previous decisions is allowed in this sequential approach. Thus, location-allocation decisions have a great impact on the final solution and, at the same time, both tactical and operational decisions depend on the distribution network that is defined during the first step of the approach. On the right hand side of the Figure 1, we have the integrated approach. Here we can note that information flow from one decision level to the other.

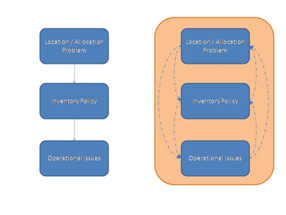poza_artFigure 1. Traditional sequential approach (on the left) versus the integrated approach (on the right)

This means that strategic decisions are made taking into account the effects that such decisions provokes at tactical and operational levels. As a consequence, the final solution is more efficient in terms of its total system cost.

The remaining of this paper is as follows: In Section 2 the inventory location modelling problem that is addressed in this paper is presented.

In Section 3 we introduce the evolutionary algorithm that is implemented here. In Section 4, the computational experiments performed in this paper are described and the obtained results are discussed. Finally, in Section 5, some conclusions and the future work are outlined.

REFERENCES

  1. AHMADI, G., S. A., TORABI, R. TAVAKKOLI-MOGHADDAM, A Bi-Objective Location-Inventory Model with Capacitated Transportation and Lateral Trans-shipments, International Journal of Production Research, 2015, pp. 1-22.
  2. ARABZAD, S. M., M. GHORBANI, R., TAVAKKOLI-MOGHADDAM, An Evolutionary Algorithm for a New Multi-Objective Location-Inventory Model in a Distribution Network with Transportation Modes and Third-Party Logistics Providers, International Journal of Production Research, vol. 53(4), 2015, pp. 1038-1050.
  3. ARMENTANO, V. A., A. L. SHIGUEMOTO, L. A., LOKKETANGEN, Tabu Search with Path Relinking for an Integrated Production-Distribution Problem, Computers and Operations Research, vol. 38(8), 2011, pp. 1199-1209.
  4. ASKIN, R. G., I., BAFFO, M., XIA, Multicommodity Warehouse Location and Distribution Planning with Inventory Consideration. International Journal of Production Research, vol. 52(7), 2014, pp. 1897-1910.
  5. BRADLEY, J. R., B. C. ARNTZEN, The Simultaneous Planning of Production, Capacity, and Inventory in Seasonal Demand Environments, Operations Research, vol. 47(6), 1999, pp. 795-806.
  6. CABRERA, G. G., E. CABRERA, R. SOTO, L. J. M. RUBIO, B. CRAWFORD, F. PAREDES, A Hybrid Approach Using an Artificial Bee Algorithm with Mixed Integer Programming Applied to a Large-Scale Capacitated Facility Location Problem, Mathematical Problems in Engineering, vol. 2012, Article ID 954249, 14 pages, 2012.
  7. CABRERA, G., G., P. A. MIRANDA, R. E., CABRERA, R. SOTO, L. J. M. RUBIO, B. CRAWFORD, F. PAREDES, Solving a Novel Inventory Location Model with Stochastic Constraints and Inventory Control Policy, Mathematical Problems in Engineering, vol. 2013, Article ID 670528, 12 pages, 2013.
  8. DASKIN, M. S., C. R. COULLARD, Z. M. SHEN, An Inventory Location Model: Formulation, Solution Algorithm and Computational Results, Annals of Operations Research, vol. 110, 2002, pp. 83-106.
  9. HOLLAND, J. H., Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor, Michigan, USA, 1975.
  10. LAGOS, C., F. PAREDES, S. NIKLANDER, F. E. CABRERA, Solving a Distribution Network Design Problem by Combining Ant Colony Systems and Lagrangian Relaxation, Studies in Informatics and Control, vol. 24(3), 2015, pp. 251-260.
  11. MIRANDA, P. A., R. A. GARRIDO, Incorporating Inventory Control Decisions into a Strategic Distribution Network Design Model with Stochastic Demand. Transportation Research Part E, Logistics and Transportation Review, vol. 40(3), 2004, pp. 183-207.
  12. MIRANDA, P. A., R. A. GARRIDO, A Simultaneous Inventory Control and Facility Location Model with Stochastic Capacity Constraints, Networks and Spatial Economics, vol. 6, 2006, pp. 39-53.
  13. MIRANDA, P. A., R. A. GARRIDO, Valid Inequalities for Lagrangian Relaxation in an Inventory Location Problem with Stochastic Capacity. Transportation Research Part E: Logistics and Transportation Review, vol. 44(1), 2008, pp. 47-65.
  14. MOURITS, M., J. M. EVERS, Distribution Network Design: An Integrated Planning Support Framework, International Journal of Physical Distribution & Logistics Management, vol. 25, 1995, pp. 43-57.
  15. OSZEN, L., C. R. COULLARD, M. S. DASKIN, Capacitated Warehouse Location Model with Risk Pooling, Naval Research Logistics, vol. 55(4), 2008, pp. 295-312.
  16. SHEN, Z. M., C. R. COULLARD, M. S. DASKIN, A Joint Location Inventory Model, Transportation Science, vol. 37(1), 2003, pp. 40-55.
  17. SIMCHI-LEVI, D., Y. ZHAO, The Value of Information Sharing in a Two Stage Supply Chain with Production Capacity Constraints, Naval Research Logistics, vol. 50(8), 2003, pp. 888-916.
Designed by | ICI Bucharest
© Copyright 2024, All Rights Reserved